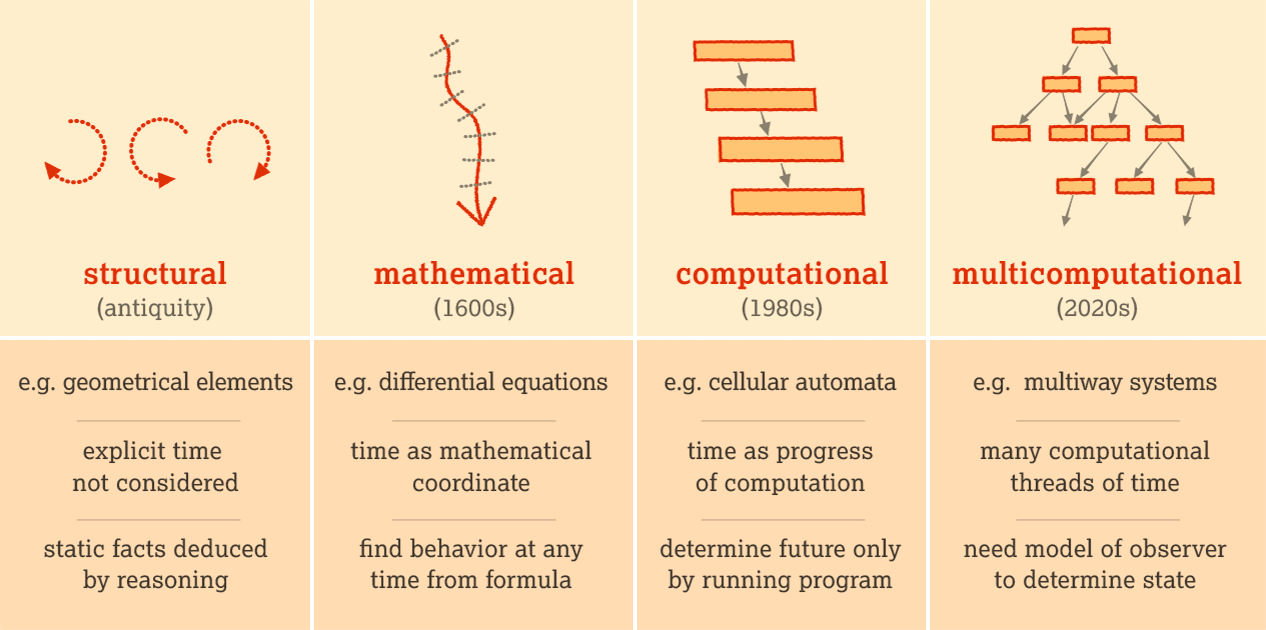
Understanding Emergence
This work began as a study of the phenomena captured beautifully by the notion of “emergence” and developed into an elegant theory of the physics of self-organisation. It combines Wolfram and Friston’s mathematical frameworks with complexity theory to better characterise the idea of a “universal assembly function”.
If you trace the origins of the Simulation Hypothesis back to Konrad Zuse’s Rechnender Raum (“Calculating Space”, 1969) you uncover an interesting area of digital physics that relates to solving for the evolutionary function of the universe, by treating it as a vast computational system.
Decades before McCarthy conjectured that “every aspect of learning or any other feature of intelligence can in principle be so precisely described that a machine can be made to simulate it,” Zuse imagined that the universe behaves like a vast computer, ceaselessly executing formal rules to compute its own evolution.
At the heart of this perspective lies the concept of emergence — when novel patterns and properties arise from complex systems that did not exhibit those properties before. Given its profound implications, and how it feels like the closest thing to magic that science can admit, emergence is a concept that flies surprisingly under the radar even within academia.
Emergence describes the creation of new behaviours that seem to transcend the sum of their parts, and it succinctly describes the causal chain from the formation of matter to human abstraction. Let’s quickly map this in accordance to Nick Lane’s Life Ascending (see [1] for a detailed timeline):
-
Distribution of mass energy → spacetime curvature (Unlock: gravity).
-
Subatomic articles + gravity → atoms and molecules (Unlock: chemical bonding)
-
Hydrogen + oxygen molecules (as gases) → H₂0 (liquid at room temperature).
- Complex organic molecules → Self-replicating RNA (Unlock: life)
- Living cells self-replicate, despite no solo molecule respiring, reproducing or metabolising.
- Living cells self-replicate, despite no solo molecule respiring, reproducing or metabolising.
- Single-cellular organisms + Gene transfer → Multicellular organisms
- Sex permits greater genetic differentiation in tissues and organs within organisms.
- Sex permits greater genetic differentiation in tissues and organs within organisms.
- Specialised cells + photoreceptors → Simple nervous systems (Unlock: wakingness)
- The Cambrian diversity explosion followed organisms gaining proper eyes.
- The Cambrian diversity explosion followed organisms gaining proper eyes.
- Basic nervous systems → Reptilian brain → Mammalian brain → Neocortex
- Sophisticated cognitive abstraction available at ~86 billion neurons + trillions of synapses.
- Sophisticated cognitive abstraction available at ~86 billion neurons + trillions of synapses.
- Individual humans + Language + Technology → Civilisations (Unlock: global intelligence)
Each layer of physical reality exhibits emergent properties that transcend its constituent parts, in a type of hierarchy known as holarchy. The same reality we evolved in is primed for this emergence, with all of our most basic physical laws emerging from simpler foundations. Gravity emerges as the geometric consequence of mass-energy’s influence on spacetime, while time emerges simply as the direction in which disorder increases, giving rise to our experienced flow from past to future.
This pattern extends upward through layers of increasing complexity with different properties appearing. Intelligent behaviour emerges from neural networks that individually exhibit no such behaviour (shown below). Social structures emerge from individual behaviors, giving rise to cities, nations, and global movements. Each new layer of complexity displays properties unobserved in its components. [2]
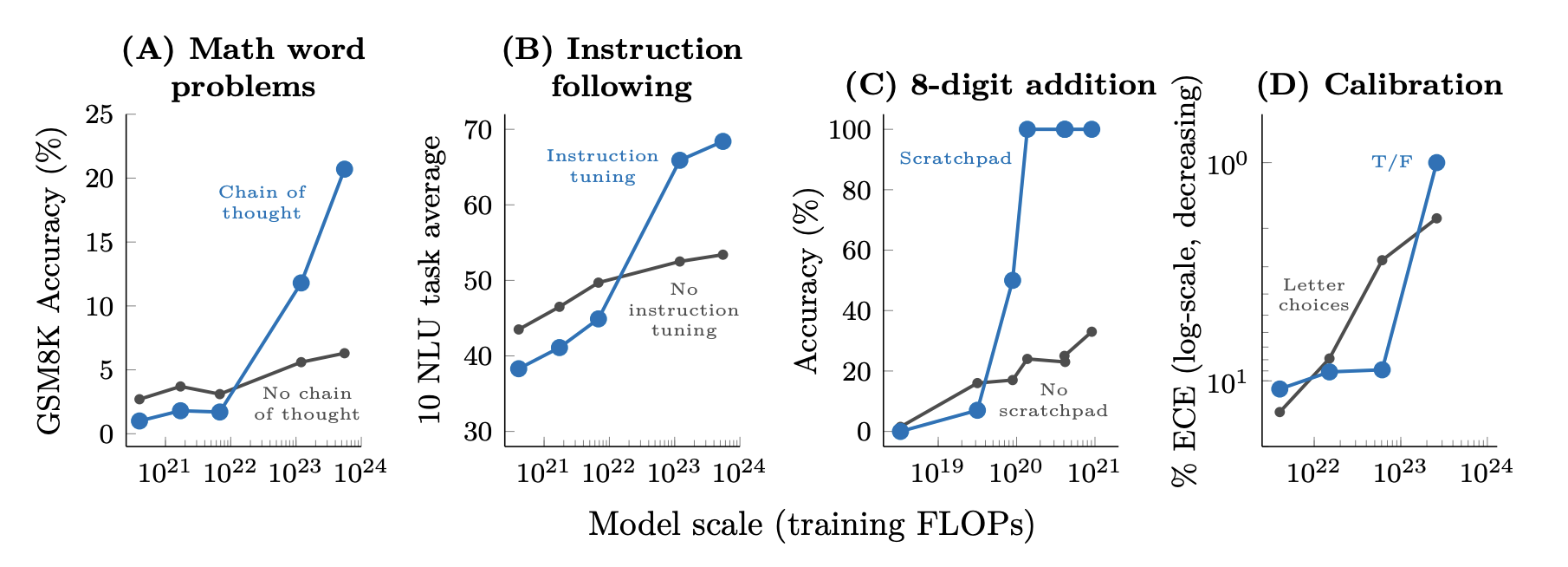
For instance, the emergent intelligence exhibited by neural language models only appears at certain thresholds; each level hard-coded by some physical law that applies to the architecture and training regime. [3]
Elegance Over Entropy
At the heart of emergence is the notion that nothing evolves in a vacuum; everything evolves gradually and synergistically. Neither the chicken or the egg came first if they both developed in conjunction.
In the eyes of complexity theory, all objects hold a mixture of:
-
Entropic relationships: whereby no new properties emerge, or properties are destroyed (the tendency towards disorder).
-
Synergistic relationships: these give rise to new properties and structures, driving ‘emergent complexity’ (the tendency to resist disorder).
Daniel Schmachtenberger describes synergistic relationships as “more elegantly ordered complexity”, which is the universe self-selecting for (1) increasing diversity, coupled with (2) more synergistic combinations across that diversity. In this sense, evolution is not merely about the traditional notion of ‘survival’, but about the creation of ever more interconnected systems that favour new properties of greater sophistication.
To illustrate synergy and complexity, we’ll use a paper from 2007 called Picbreeder. Users who visited the website could evolve pictures by applying sine, sigmoid, linear or gaussian convolutions on an image. As branches are evolved, they become explicitly more complex (there is no ability to devolve the images), and this reliably adds complexity with every step (c).
Interestingly, however, this isn’t always the story. In (d), relationships discovered by users show intelligible complexity, with cars, sunsets, species, and planets forming under the same conditions as everything else, creating immense synergy and beauty.
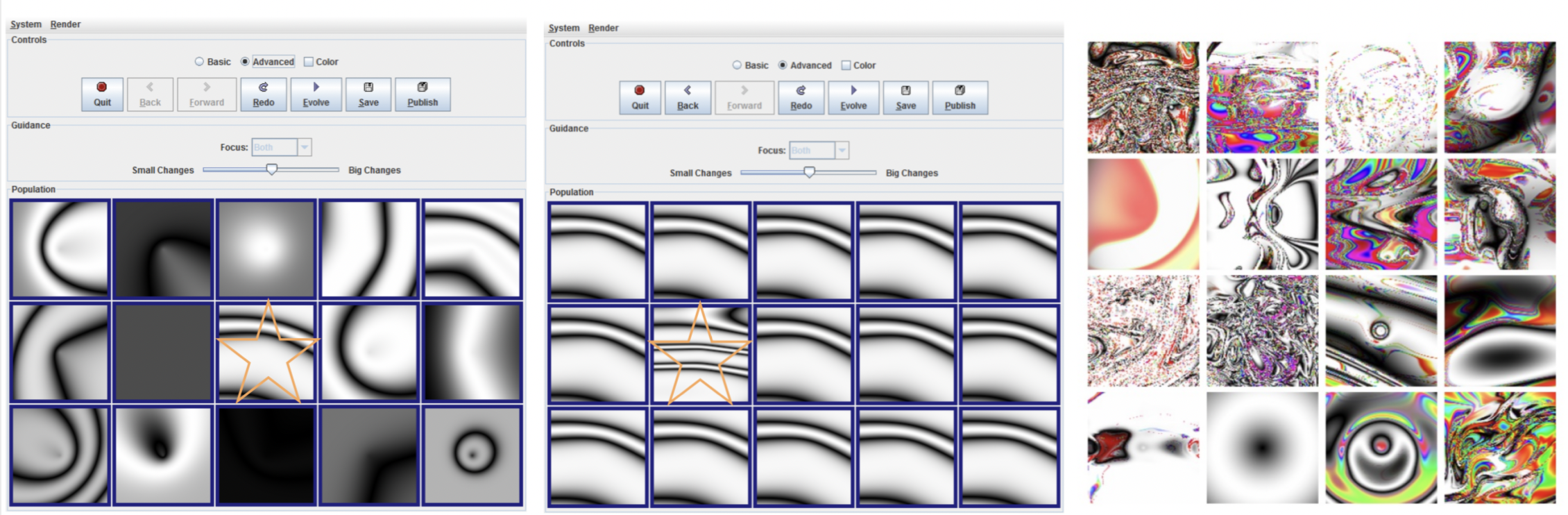
(a and b): Process of selecting and evolving images is simple.
(c): Images become very complex with enough steps.

(d): Emergent complexity (cars, species, planets) forming at the meso scales of evolution.
Three important observations:
-
Evolution in Picbreeder is one-directional; the states that can evolve into, e.g., cars, will not evolve into more simple states using the same functions applied. This is known as ‘divergency’, and seems to be a property of the material universe we inhabit [4].
-
Later-states are not obviously predictable; when one tries to produce a car, one will struggle to achieve this without trial and error. In other words, mastering Picbreeder is very hard.
-
Intuitively, the “emergent complexity” we observe seems highest in the meso-stages of evolution (the images shown in (d) are only momentary snapshots of longer branches that eventually become disordered).
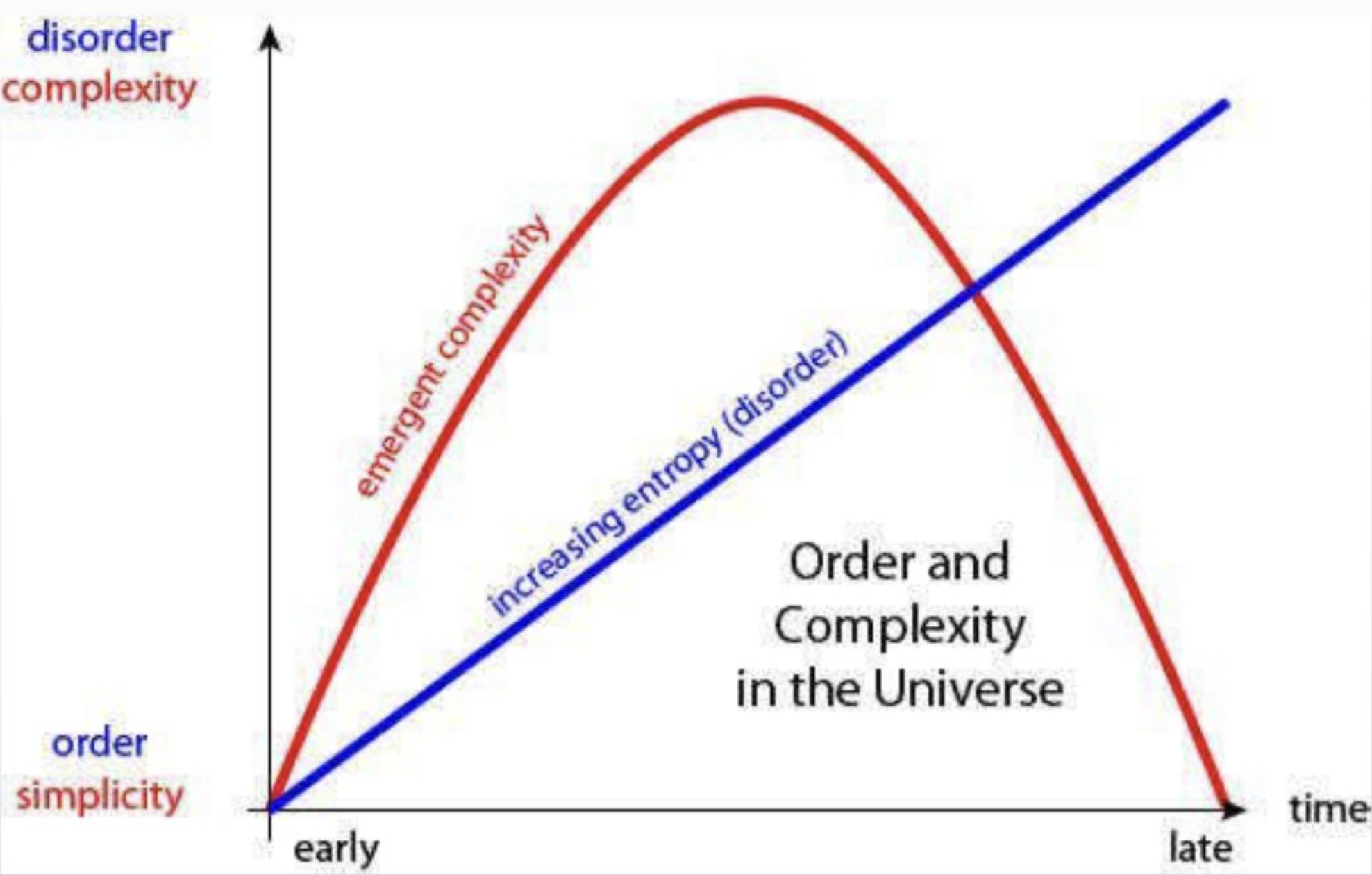
Dynamical systems generally exhibit emergent complexity in the meso-stages when things are changing fastest. Interestingly, entropy generally only ever increases, eventually tending towards homogeneity at equilibrium when the process settles. [5]
In the eyes of Professor Karl Friston, systems that persist over time must do more than just resist entropy — they actively self-organise. At the heart of this self-organisation is what he calls the ‘free energy principle’: the idea that surviving systems naturally minimise uncertainty in their interactions with their environment.
In non-living systems, this manifests as the process that shapes systems toward more stable, lower-energy configurations. A water droplet forming a sphere, a crystal growing in a supersaturated solution, or atoms arranging themselves into molecular structures –– all of these can be viewed as systems minimising their free energy by finding configurations that best match the constraints of their environment.
In organisms, this manifests as ‘active inference’, where organisms seek to reduce the error between predicted and actual sensory inputs. They do this either by seeking out or building environments that match their adaptations (their ‘internal Markov state’), or by developing increasingly sophisticated internal models to handle environmental uncertainty (sensors, instincts, abstraction and the capability to plan). More on this in part 8.
Weak and Strong Emergence
In order to understand emergence, we must study the properties of dynamical systems. We will use a recent formalisation by DeepMind (2024), in their paper on open-endedness.
- Novelty: A system possesses novelty when it consistently produces artifacts that become less predictable over time with respect to the observer’s existing models.
- Learnability: A system is learnable when access to more historical data makes its artifacts more predictable - in other words, observation improves understanding.
By this token, our ability to interpret novel systems is a reflection of the capacity of our cognitive substrate to comprehend how these systems work. While some emergent phenomena are readily comprehensible, others prove stubbornly resistant to human understanding. This cognitive boundary helps explain the law of diminishing returns in scientific discovery — as the low-hanging fruit become sparse, progress would require exponentially more work for any observer, provided they do not upgrade their cognitive faculties.
When it comes to emergent complexity, we find that this lies along another spectrum:
- Weakly emergent properties: while novel, future states can be readily predicted given an understanding if the underlying components and their interactions. For example:
- Simple molecular properties: The hardness of diamond is a product of the strong covalent bonds in the carbon lattice structure that it consists of. The idea that diamond would be hard is learnable to anyone with the ability to comprehend molecular bonding. This was once an unknown scientific phenomena, but the relationship is now well understood.
- Low-energy superconductivity: Certain materials at low temperatures exhibit zero electrical resistance and perfect diamagnetism (the Meissner effect). This phenomenon was first predicted theoretically by BCS theory before being verified experimentally. This collective behavior can be explained and predicted using quantum mechanics and solid-state physics.
- Fluid dynamics: The chaotic behavior of turbulent fluid emerges from particles following simple Newtonian laws of motion. While individual particle interactions are straightforward, their collective behaviour produces complex patterns like vortices, eddies, and turbulent flows which can be modeled with the Navier-Stokes equations. Given sufficient computing power and initial conditions, these are predictable phenomena.
- Simple molecular properties: The hardness of diamond is a product of the strong covalent bonds in the carbon lattice structure that it consists of. The idea that diamond would be hard is learnable to anyone with the ability to comprehend molecular bonding. This was once an unknown scientific phenomena, but the relationship is now well understood.
- Strongly emergent properties: cannot be readily explained from the sum of their parts, meaning they remain thoroughly intractable or unpredicted by state-of-the-art models developed by humans. These properties seem to exhibit “downward causation,” where higher-level phenomena influence their lower-level constituents in ways that appear irreducible to simple component interactions. Examples include:
- Consciousness: Predicting a lived experience in any complex system seems to be a problem for the ages; no matter how well we seem to understand the structure of the brain, we can’t seem to explain convincingly why any physical state is conscious of its own physical state, and not unconscious. A unified theory of substrate independence would need to differentiate between all systems; to explain the consciousness of a raincloud and the sentience of a human or artificial brain. [6]
- Room-temperature Superconducitivity: Unlike low-temperature superconductivity, room-temperature superconductors remain largely unpredictable. Recent claims about LK-99 continue to lack comprehension of how materials can exhibit this property and the degree to which it can be harnessed by man.
- The quantum-to-classical transition: How quantum superposition gives way to definite classical states is another one of physics’ more profound puzzles. While decoherence theory provides some insights, the complete mechanism continues to challenge our understanding of fundamental physics (known as the measurement problem).
- Abiogenesis: The emergence of life from non-living matter remains strongly emergent. There is no consensus on the order of events that catalysed self-replicating molecules to form, and we do not know what components are universally essential. Until we can activate multiple trees of life within the lab, this will remain poorly understood.
- Consciousness: Predicting a lived experience in any complex system seems to be a problem for the ages; no matter how well we seem to understand the structure of the brain, we can’t seem to explain convincingly why any physical state is conscious of its own physical state, and not unconscious. A unified theory of substrate independence would need to differentiate between all systems; to explain the consciousness of a raincloud and the sentience of a human or artificial brain. [6]
- Absolute emergence: If something were to be absolutely emergent, it would need to hold that no future system of science or computation could foretell such properties. The notion that there are behaviours that cannot be explained by science remains an open question.
The scientific process parses unknown dynamics into a language humans can make predictions with. When a theory is able to predict results that can be tested experimentally, it has the potential to be extremely strong. Take Bose-Einstein condensation, predicted in 1924 as a new state of matter where atoms collapse into their lowest quantum state: it took until 1995 to observe this experimentally. Similarly, the Higgs Boson was predicted in 1964, and only found in 2012. These are elegant theories that continue proving their potential as technology catches up.
Gravity and biological diversity were strongly emergent properties, understood only intuitively until Einstein and Darwin, who would each make predictions long before they could be tested by gravitational wave telescopes or protein sequencing. Even off the back of the discovery of DNA, protein folding would remain largely misunderstood until 2020, where with computer assistance, we went from understanding around 17% of human protein structures (just 4,000 structures) to well over 200 million structures across 1 million species: a 1000-fold update in the field.
The same goes for artificial intelligence, which did not harness emergent behaviour like deep learning until the inception of AlexNet. Sutton’s Bitter Lesson seems to be a universal governing principle for any problem that requires searching through dynamical systems in order to learn them [7].
Our relationship with learning machines appears to offer new life for science by passing on the bulk of the computational burden to our silicon counterparts, allowing us to stretch what humanity can learn. These machines ‘solve’ problems in ways that no single human mind would have the capacity to compute, which allows us to build technology to better service our needs.
We can use this to define three components of progress for civilisation:
-
The frameworks and languages we use to understand dynamical systems.
-
The methods we use to make the novel systems learnable (like AI).
-
The tools we build to harness this new knowledge.
For the first, we favour compression and elegance. For the second we favour the ability to learn novel systems. For the third, we favour moral frameworks of utility and empathy (among other things).
For the rest of this essay, I will focus on the language we use to describe dynamical systems.
The Language of Emergence
What matters when it comes to language and what are we missing when we fail to interpret dynamical systems?
Take the Mandelbrot set, which is often used to illustrate the trade-off between static languages and computation. We often communicate these fractals in image form, like the one below. Storing the 24-bit colour of each pixel in this image would require 23 million bytes, but an image would be useless at capturing the dynamic nature of the set unless you could zoom in infinitely.
Suppose, then, we zoomed in, capturing every new structure at every magnification. This effort would only be as useful as the number of pictures you take — which would eventually take up all the memory available in a finite universe and still fail to capture the full nature of the system.

Without capturing the dynamic nature of a Mandelbrot, any approach you used would be meaningfully deficient [8].
Let’s suppose instead that you could encode the recursive function of the Mandelbrot set into your program, so that now a far small computer program could reproduce this image in 100 or 1000 bytes. Now you would successfully upgrade your representation to one that would be able to inform both the image AND the fractal nature of the Mandelbrot set.
Now observe how this applies to us: we build theories that have the effect of photographing the Mandelbrot set. We aren’t paying attention to the generating function that underlies everything we observe.
One way to formally evaluate the sophistication of our descriptions is through Kolmogorov complexity — defined as the length of the shortest computer program that can produce a given output. This metric helps distinguish between superficial descriptions and fundamental understanding. A description with low Kolmogorov complexity relative to its output suggests we’ve captured something essential about its generating process. For example, the entire Mandelbrot set can be defined in remarkably concise (english) language of 165 characters:
the set of complex numbers c for which the function f(z) = z² + c
does not diverge when iterated from z = 0
with coordinates: (0,0), (802, 0), (0, 602), (802, 602)
This brings us to the fundamental challenge of emergence: How can we study systems that become more complex with each step?
The answer to this lies in what we might call “computational compression”: finding the shortest possible description that captures not just the state of a system, but also its entire possibility space. Like making a Kolmogorov complexity metric by treating the universe as discrete, in order to measure the assembly function responsible for all the behaviour we see in the natural universe.
Computational Science
In Stephen Wolfram’s 2002 book “A New Kind of Science,” he proposed describing the universe as a network of interconnected points where the ‘laws of physics’ emerge from the rules that update the connections in this network (more on this shortly). This forms part of what he calls “Rulial Space”: the abstract hyperobject of all possible rules that could govern such a system. This object would be ‘computable’, meaning an update rule could be found that describes all transformations that occur within the known universe.
A graph-wise demonstration of this is performed below, where each new transformation has the same condition applied to it, recursively. A set of rules will propagate ad infinitum and create ever-larger structures. Wolfram then runs this for the below computation 1000 times and discovers an emergent, cone-like geometry.
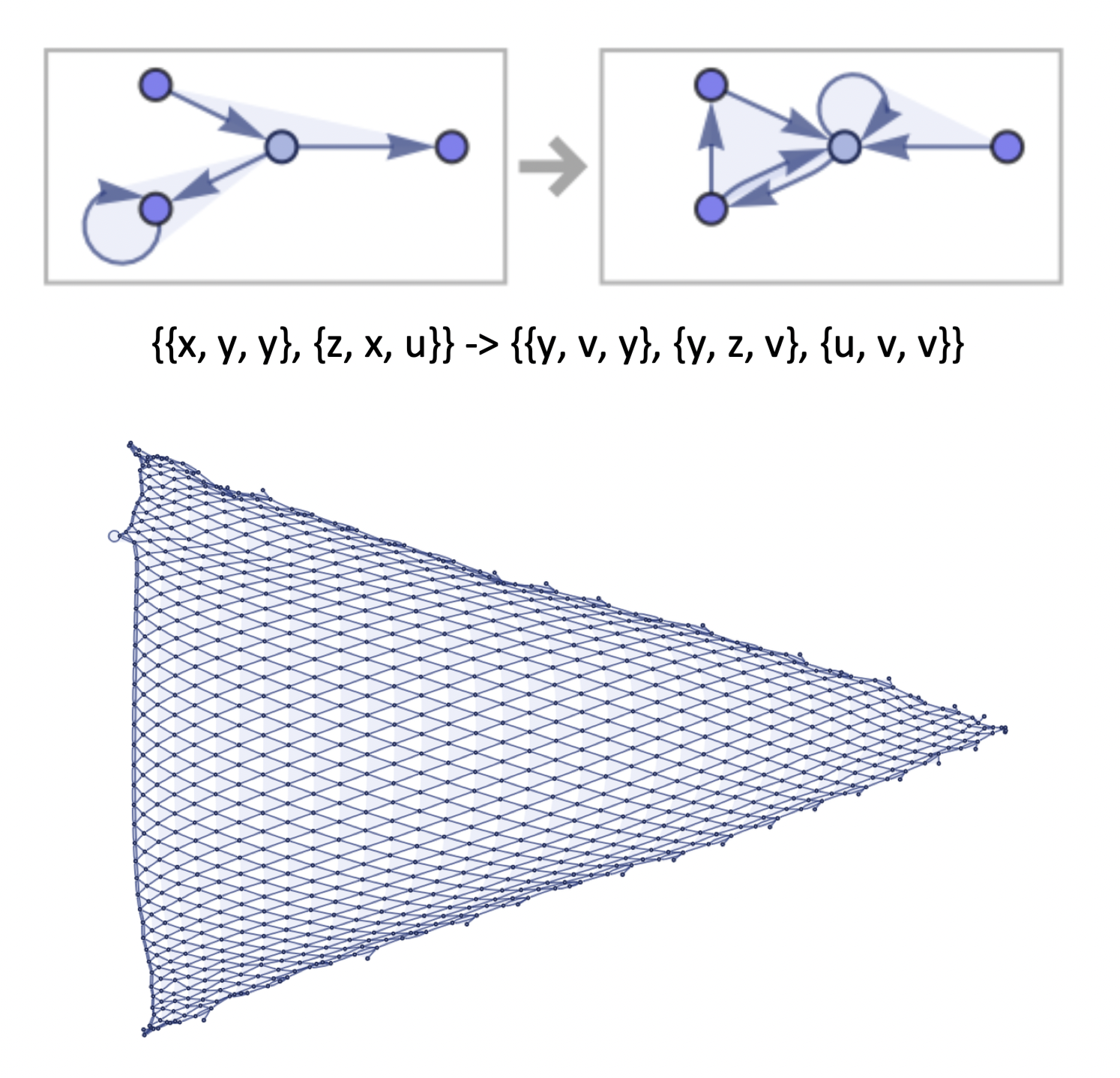
A slightly different rule produces even more curious behaviour, and a whole taxonomy of ‘species’ can be observed when many rules are activated in parallel.
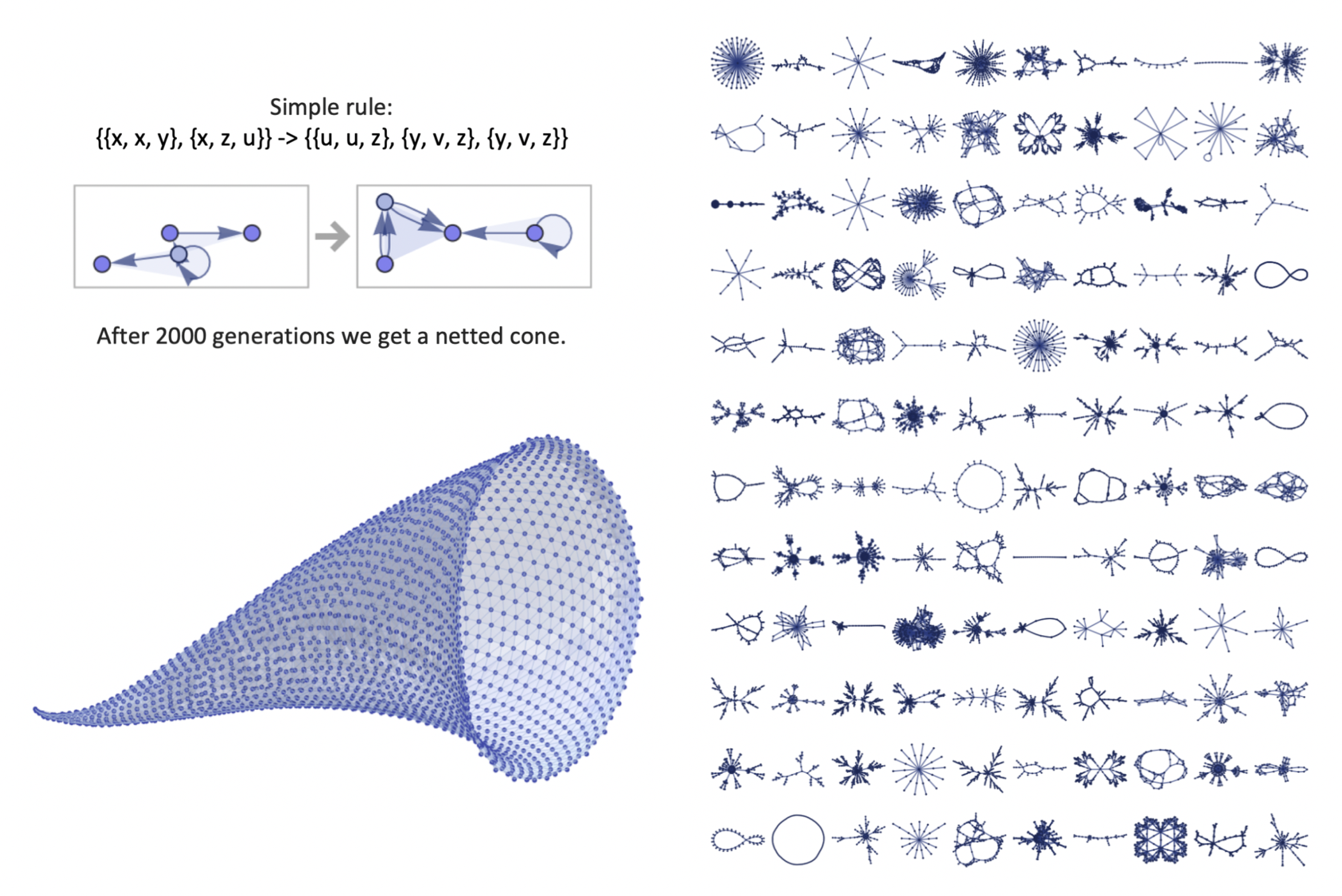
Wolfram has long proposed using discrete graphs to describe the universe. Until 2020, his graph-based theory was met with scepticism by physicists due to its incompatibility with Einstein’s theories of general relativity, which violated some spacetime symmetries like Lorentz-invariance. However, Wolfram has more recently described Rulial Space as a hypergraph, meaning the links have no physical length and can link multiple points simultaneously. This approach is compatible with Lorentz-invariance, similar to how Rafael Sorkin discretised spacetime within “Causal Sets” while preserving its essential properties. [9]
Multicomputation
Unlike regular computation which follows a single thread through time, multicomputation supports multiple interwoven threads of time, which would better characterise emergence in the physical universe.
Now the story becomes: observers like us “parse” their relative multiway system when they make observations. This creates different possible reference frames that must be “computationally bounded”, meaning they can’t require unlimited computation to construct. These reducible ‘slices’ force certain generic laws to persist, and these laws end up being analogous to physics concepts like general relativity and quantum mechanics.
At the moment, the way Wolfram describes the discrete nature of the universe is by referring to the axiomatic “carriers of state” that persist between events as “tokens”. These tokens are parsed by events that perform transformations on the present hyperstate. Each token can be uniquely identified by its connected nodes, and these evolve as events occur.
Events are characterised by the input tokens and the function they enforce. They can be classed in accordance to three main types of separation:
-
Spacelike separation: With respect to the independence of other events executing in-parallel,
-
Timelike separation: With respect to when event occurs in-sequence; identified by what tokens the function uses as input,
-
Branchlike separation: With respect to the quantum-like superposition of possibile events,
-
A fourth property describes Rulial computation only, and separates events in the wider multiverse by the rules that apply (Rulelike separation)
The power of this framework lies in its potential applications beyond physics. Just as statistical mechanics and quantum mechanics provided frameworks for understanding complex systems, multi-computation offers a way to understand emergence across different domains. I want to try and express why I find it so powerful.
Analysis of Multicomputation
The foundation of traditional mathematics rests on ZFC (Zermelo-Fraenkel Set Theory with Choice) — a formal system built from nine axioms that define how sets behave (e.g. Empty Set, Pairing, Union, Power Set, Infinity, etc.). What makes ZFC remarkable is its economy of expression — it represents perhaps the most successful attempt to compress the vast landscape of mathematical truth into a small set of foundational principles.
But two important results, made in the last hundred years, show us the foundational limitations of this framework. Interestingly, we are the first civilisation to have an understanding of mathematics with respect to these basic properties:
-
Turing showed that while computational systems can achieve universality — “Turing completeness” — they inevitably encounter the Halting Problem. This limits algorithms from being able to determine whether arbitrary programs will terminate. Note: this isn’t a limitation we can overcome with better programming or more powerful computers; it represents an absolute bound on what sequential computation can achieve.
-
Gödel showed in his First Incompleteness Theorem that in any consistent formal system powerful enough to encode basic arithmetic, there exist true statements that cannot be proven within that system. His Second Incompleteness Theorem then delivers an even more powerful result: such systems cannot prove their own consistency. Together, these theorems reveal a fundamental trade-off: mathematics cannot simultaneously achieve both completeness and consistency within any fixed axiomatic framework.
The elegance of multicomputation lies in how it transforms these apparent limitations into natural features. By considering all possible rules simultaneously, the Halting Problem transforms from a system limitation into a statement about observer capabilities. Similarly, Gödel’s incompleteness becomes a natural features of how different observers, with their computational bounds, can access different “true but unprovable” statements. This shifts our perspective from seeking absolute mathematical truth to understanding how observers can access different, equally valid realities.
In other words, multicomputation is not merely looking at “given states” where time is a variable, it is looking at all possible whole histories for the system. It is designed to capture the evolution that occurs before arriving at the given state, and where it will go next. It describes what an observer sampling the whole multicomputational process would perceive. [10]
This reframing ought to have profound implications for how we approach complex problems across disciplines. Instead of trying to reduce systems to their simplest axioms, we can study how different observational frameworks reveal the objective axioms of complexity in the universe.
Universal Pattern Matching (MESA Theory)
How can one develop a multicomputational model to describe emergence?
The answer lies in applying our understanding of how systems self-organise and minimise free-energy with respect to the lens of multicomputation. We’ll use these branches, along with assembly theory to introduce a theoretical framework called MESA (Multicomputational Emergent Self-Assembly) to unify these ideas.
Free Energy
The free energy principle, first conceived by Hermann von Helmholtz and more recently by Karl Friston, provides the thermodynamic foundation. It states that any system maintaining its own organisation can be modeled using a Markov blanket: a statistical boundary that separates internal states from external influences.
Friston’s free energy principle (abstracted from von Helmholtz) suggests any system that maintains its organisation can be modelled as an internal state within a Markov blanket.
-
(μ) Internal states (the system configuration, running active inference to minimise surprise)
-
(η) External states (information flowing across the Markov blanket; the environment):
-
(s) Sensory states (influences from outside)
- Update internal models about external conditions
- Update internal models about external conditions
-
(a) Active states (the system’s influence on its environment)
- Attempts by internal state to make sensory inputs match predictions
-
These boundaries explain how depth tends to develop most robust protective mechanisms against entropy, and this manifests in several key ways:
Temporal persistence: the duration of the update horizon increases with depth. This means more complex systems can make predictions further into the future, with more sophisticated planning.
Multicomputation
Multicomputation provides the computational framework that complements the free energy principle through its token-event structure. In this framework, tokens represent states within Markov blankets, while events describe the transformations that minimise variational free energy over time.
-
(ψ) Tokens: carriers of state within Markov blankets.
-
(ε) Events: transformations minimising F over time.
-
The event separation types correspond to different aspects of free energy minimisation:
-
Timelike (εₜ): sequential gradient descent on F
-
Spacelike (εₛ): parallel active inference processes
-
Branchlike (εᵦ): alternative predictive paths
-
We can model the structure and behaviour of any complex system by its “tokens” and “events”, where whole histories demonstrate how tokens are entangled. Any laws we observe emerge from this fundamental drive toward self-evidencing organisation, as they are the rules that characterise all of its emergent properties.

(a) Markov blanket as centred around by free-energy theory,
(b) Multicomputational ‘events’ and ‘tokens’ for nine fields.
This framework makes several key properties of complex systems seem natural:
-
Entangled layers: Markov blankets aren’t simply nested in levels but are deeply entangled, where information flows both up and down the hierarchy through gradient fields.
-
Gradient flows describe how systems follow paths of least action in their state space.
-
Multiple gradient fields interact simultaneously; free energy gradients guide system evolution, information gradients shape knowledge propagation, complexity gradients drive emergence of new properties.
-
-
Multiway influence: Lower-level properties emerge from and constrain higher-level organisation so each level inherits constraints while developing new emergent properties.
-
Entropy resistant: Systems resist entropy by achieving structural stability through multiple complementary mechanisms, most notably:
-
Maintaining multiple parallel predictive paths (branching redundancy).
-
Hierarchical feedback loops with varying temporal persistence.
-
Assembly
Assembly theory provides the quantitative metrics for measuring emergence and gives physical meaning to the patterns we observe in multicomputational systems. It suggests two fundamental measures:
-
(β) Copy number: The prevalence of a particular configuration
- Acts as a selection pressure for stable configurations
- High copy number suggests robustness against perturbation
- Helps distinguish meaningful emergence from statistical fluctuations
-
δ Assembly index: The minimum number of steps required to construct an object
- Reflects historical path-dependency of formation
- Captures computational irreducibility of complex systems
- Increases with organisational complexity
We can formalise this with an emergence coefficient (ε) that combines these metrics;
ε = δ × log(β)
Where emergence is a product of both the complexity of assembly (δ) and the logarithm of its reproducibility (β). The logarithm prevents extremely common but simple configurations from dominating the measure.
This helps explain several key phenomena:
-
Path Dependence: the work done (W) to achieve depth δ follows a power law: W ∝ δᵏ where k > 1 reflects increasing difficulty of maintaining higher complexity.
-
Stability Thresholds: Systems require minimum breadth (β_min) to persist: β_min ∝ exp(δ/c), where c is a system-specific constant reflecting environmental constraints.
-
Information Processing Capacity: Maximum predictive horizon (τ) scales with depth: τ ∝ log(δ), reflects increased temporal persistence in complex systems.
Thus emergence isn’t just about complexity or prevalence alone, but the balance of sophistication and reliability of reproduction. Natural selection operates on this emergence coefficient, favoring systems that maximise ε within their environmental constraints.
MESA Theory: Applications
This unified approach models the universe as a dynamic system self-organising into observers that parse reality in ways that minimise their internal uncertainty.
-
Structure (“what”): The token-event structure of multicomputation provides the mathematical language for representing states within Markov blankets.
-
Process (“how”): Free energy minimisation explains how certain configurations persist while others dissolve.
-
Measure (“why”): Assembly metrics quantify which structures are likely to emerge and remain stable.
Applying MESA Theory:
MESA theory can be used to model Efficient Markets, learning rules, linguistics, chemical interactions, and possibly everything else.
But for now, let’s use this theory to describe how biological systems self-organise into increasingly complex hierarchies while maintaining stability:
[See Appendix for our example]
Conclusion
MESA (Multicomputational Emergent Self-Assembly) theory provides a unified mathematical framework for understanding how complex systems self-organise and evolve. By combining three powerful approaches—multicomputation, free energy principles, and assembly theory—it offers a complete language for describing emergence across all scales.
- Structure (“what”): Token-event multicomputation grammar provides the mathematical language for representing states within Markov blankets
- Process (“how”): Free energy minimisation describes how configurations persist or dissolve through active inference
- Measure (“why”): Assembly metrics quantify the likelihood and stability of emergent structures through depth and copy number
This framework reveals how nature builds complexity through nested layers of organisation, each inheriting constraints while developing new properties. Systems resist entropy through multiple complementary mechanisms, and advancing science requires better understandings of the nature of our universe.
- Physical systems; quantum decoherence into classical behavior, crystal formation and phase transitions, self-organising critical phenomena.
- Chemical systems; molecular self-assembly, reaction-diffusion patterns, autocatalytic networks.
- Biological systems; protein folding landscapes, cellular differentiation, neural development.
The challenge ahead lies not in describing what has emerged, but in predicting what will emerge. These examples may seem simple, but they represent necessary steps toward understanding the mathematical principles that govern emergent complexity itself.
References
[1] The Ascent of Man (in more detail):
- Quarks combine to form hadrons, exhibiting the emergent property of colour confinement.
- Spacetime curvature emerges from the distribution of mass-energy, giving rise to gravity as a geometric property.
- From particles, atoms and molecules emerge as a result of gravity, despite that fact gravity isn’t present in any single particle.
- All chemistry thereafter is alchemy: molecules of hydrogen and oxygen bind as gases to create a liquid at room temperature.
- Biological systems emerge from a complex organic molecules. Living cells self-replicate, despite the fact molecules do not respire, reproduce or metabolise.
- Sexual reproduction emerges to mix longer sequences of genetic material between organisms, and permits greater differentiation in tissues and organs within organisms.
- Advanced sensory processing in organs leads to simple nervous systems, which become more complex and capable of feeling emotion.
- The human brain emerges with the capability of abstraction through the complex interplay of ~86 billion neurons and trillions of synapses.
- From here, human civilisation emerges as a synergy of technology and culture.
[2] This same pattern was present in the earliest moments of the universe: before gravity emerged as a distinct force, the interplay of quantum fields exhibited their own forms of emergence. And probing further back, theoretical physics suggests a state preceding the very emergence of time itself, where our conventional notions of temporal sequence may not apply.
Scientists are actively exploring pre-matter by searching for specific patterns of polarisation in the CMB called B-modes using the BICEP and Plank telescopes, and proposed telescopes like LISA (which I got to see Kip Thorne spoke about very excitedly in a lecture he gave at Kings College London). Detecting B-waves are one of the holy grails of cosmology. The short version of it is that CMB can be polarised, meaning the electromagnetic waves have a preferred orientation that can be decomposed into E-modes and B-modes. E-modes are produced by various processes while B-modes have a divergence-free pattern that is consistent with only the gravitational waves from the inflationary period. What’s more, B-mode detection could provide our first observational insight into quantum gravity.
Here’s another novel perspective on this: The Big Whisper Theory
[3] Emergent Abilities of Large Language Models (2022)
[4] This divergency (one-way evolution) is reflected in numerous physical phenomena. In chemistry, “disappearing polymorphs” demonstrate how matter can irreversibly evolve to more stable forms—once a more stable crystal structure is discovered, the previous form becomes increasingly difficult to produce. Similar patterns appear in biological evolution (Dollo’s law), thermodynamic systems (entropy increase), and cosmic evolution (symmetry breaking). Even in quantum mechanics, the measurement process represents an irreversible transition from quantum superposition to classical states.
[5] This relationship between complexity and entropy suggests profound implications for computational physics.
While entropy inevitably increases toward equilibrium, complex systems often display peak organisational complexity in intermediate states — a phenomenon observed across scales from molecular self-assembly to cosmic structure formation.
Kolmogorov complexity provides a formal framework for quantifying this organisational complexity, distinct from thermodynamic entropy (Aaronson, 2009).
Bostrom (2023) explores the theoretical implications of this for computational convergence, suggesting that if the universe is strongly emergent, understanding its computational principles could enable increasingly sophisticated simulation of physical processes.
This could be a reason one might use as an incentive to occupy the whole universe as a cosmic host, in order to assimilate as much matter as possible into hyper-efficient computers to get as close to solving the universe itself as physically possible.
However, practical applications would likely be more valuable at smaller scales, where computational boundaries are more tractable and immediate applications more feasible.
[6] For more of a philosophical dive, why not give David Chalmer’s Hard Problem of Consciousness a re-read with a fresh set of eyes? I found it made some arguments stand out far less impressively than before.
[7] Daniel Dennett observes that we often make tractable oversimplifications about our surroundings when we do not pay a steep price for the error rate. In other words, there was little practical benefit to upgrading from the Newtonian stance for the average person — in fact you would only learn how to calculate relativistic gravity in post-graduate theoretical physics level.
However, before The Origin of Species introduced the concept of evolution by natural selection, there were no widely believed empirical theories, and the error we paid was believing that a God created the species: a high price in the eyes of any athiest.
[8] As an aside, a sure-fire way to brick your computer is by giving a local llama a code environment and encouraging it to progressively render increasingly novel fractals and save them to your hard drive.
[9] In interest of connecting this back to Zuse and the computational universe, we should address how scientists, every few decades, reinvent the wheel on this notion; Max Tegmark proposed the Computation Universe Hypothesis (CUH), where the physical universe is not merely described by mathematics, but is a mathematical hyperstructure with four layers of complexity and can be computed.
These four layers of complexity are:
-
(I) simple conditions,
-
(II) physical constraints,
-
(III) quantum branches, and
-
(IV) other possible universes with different rules.
These follow the Spacelike, Timelike, Branchlike and Rulelike identities Wolfram defines, in that order.
As an interesting aside, after facing a lot of criticism that this would violate Gödel incompleteness, he proposed that only Gödel-complete mathematical structures have physical existence, essentially placing an upper limit on level IV complexity, and dramatically reducing the possible space of computations. This would also have the attractive side effect of explaining the ‘relative simplicity of our universe’.
It’s an interesting bug-fix that both physicists felt they had to do to calm the waters.
[10] On that topic, can we give Alex Garland his credit for this work of art that deals with this explicitly.
Appendix:
Level 3: Tissue Organisation (τ₃: years → decades)
- Assembly Metrics:
- Breadth (β₃) ≈ 10⁴ tissue types/organism
- Depth (δ₃) ≈ 10⁶ morphogenic steps
- Emergence coefficient: ε₃ = δ₃ × log(β₃) ≈ 10⁷
- System Architecture:
- Tokens (ψₜ): {cells, tissues, organs}
- Events (εₜ): {signaling, differentiation, morphogenesis}
- Markov blanket (B₃): {μ₃, s₃, a₃, η₃}
Multicomputational Dynamics:
- Timelike evolution (εₜₜ):
- Sequential developmental cascades
- Progressive tissue maturation
- Hierarchical pattern formation
- Spacelike processes (εₜₛ):
- Distributed tissue responses
- Parallel regulatory networks
- Synchronised morphogenic fields
- Branchlike pathways (εₜᵦ):
- Alternative developmental trajectories
- Compensatory repair mechanisms
- Phenotypic plasticity options
Free Energy Landscape (F₂):
- Stable attractors (∇F₃ < 0):
- Spheroid formations (min. surface tension)
- Epithelial sheets (optimal barrier function)
- Branching networks (max. surface area/volume)
- Regular cellular spacing (mechanotransduction)
- Unstable configurations (∇F₃ > 0):
- Irregular clustering (high surface energy)
- Barrier disruptions (homeostatic failure)
- Random arrangements (loss of pattern)
Level 2: Cellular Organisation (τ₂: days → months)
- Assembly Metrics:
- Breadth (β₂) ≈ 10⁸ cells/tissue
- Depth (δ₂) ≈ 10⁴ metabolic steps
- Emergence coefficient: ε₂ = δ₂ × log(β₂) ≈ 10⁵
- System Architecture:
- Tokens (ψc): {molecular assemblies, organelles, membranes}
- Events (εc): {metabolism, protein synthesis, trafficking}
- Markov blanket (B₂): {μ₂, s₂, a₂, η₂}
Multicomputational Dynamics:
- Timelike evolution (εcₜ):
- Cell cycle progression
- Sequential protein synthesis
- Membrane trafficking patterns
- Spacelike processes (εcₛ):
- Parallel metabolic pathways
- Simultaneous signaling cascades
- Distributed protein networks
- Branchlike pathways (εcᵦ):
- Alternative metabolic routes
- Cell fate decisions
- Stress response options
Free Energy Landscape (F₂):
- Stable attractors (∇F₂ < 0):
- Polarised organelle distributions
- Ordered membrane domains
- Stable cytoskeletal networks
- Unstable configurations (∇F₂ > 0):
- Random organelle dispersal
- Membrane disorganisation
- Cytoskeletal instability
Level 1: Molecular Organisation (τ₁: seconds → hours)
- Assembly Metrics:
- Breadth (β₁) ≈ 10¹² molecules/cell
- Depth (δ₁) ≈ 10² reaction steps
- Emergence coefficient: ε₁ = δ₁ × log(β₁) ≈ 10³
- System Architecture:
- Tokens (ψₘ): {conformational states, charge distributions, bond networks}
- Events (εₘ): {reactions, transitions, interactions}
- Markov blanket (B₁): {μ₁, s₁, a₁, η₁}
Multicomputational Dynamics:
- Timelike evolution (εₘₜ):
- Sequential reaction steps
- Conformational changes
- Bond formation/breaking
- Spacelike processes (εₘₛ):
- Parallel reaction pathways
- Simultaneous interactions
- Distributed energy states
- Branchlike pathways (εₘᵦ):
- Alternative conformations
- Multiple reaction routes
- Quantum superpositions
Free Energy Landscape (F₁):
- Stable attractors (∇F₁ < 0):
- Secondary structures (α-helix, β-sheet)
- Hydrophobic core packing
- Optimal binding interfaces
- Regular crystal lattices
- Unstable configurations (∇F₁ > 0):
- Exposed hydrophobic regions
- Non-optimal bond angles
- Poor charge distributions
- Steric hindrance
Hierarchical Relationships
Emergence Dynamics:
- ε = δ × log(β) [Emergence coefficient]
- W ∝ δᵏ, k > 1 [Work required for depth]
- β_min ∝ exp(δ/c) [Stability threshold]
Level Transitions (i → i+1):
- τᵢ₊₁ > τᵢ [Increasing temporal persistence]
- βᵢ₊₁ < βᵢ [Decreasing copy number]
- δᵢ₊₁ > δᵢ [Increasing assembly depth]
- εᵢ₊₁ > εᵢ [Increasing emergence coefficient]
Markov Blanket Nesting: Bᵢ = {μᵢ, sᵢ, aᵢ, ηᵢ} ⊂ Bᵢ₊₁
This hierarchical organisation demonstrates how biological systems maintain stability through:
- Nested feedback loops with increasing temporal persistence
- Multiple parallel predictive pathways (branching redundancy)
- Emergent properties that constrain and enable adjacent levels
This framework extends to evolutionary biology, where multiple possible trajectories unfold simultaneously across a fitness landscape, and to neural networks, where parallel processing creates emergent cognitive behaviours. It is exhibited in conscious systems, whereby a unified relative experience is generated by the chorus of human neurons. It is existed in economics, with EMH emerging (somewhat) from the interaction of competitive agents.